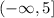Question

Find the axis of symmetry and vertex. f(x)=-x^2+5 find the domain and range.

Answer 1

`f(x)=-x^2+5`

the function represents a parabola, the equation of a parabola is

`y=ax^2+bx+c`

In our case

a=-1

b=0

c= 5

the x coordinate of a parabola can be found with the next formula

`x=-(b)/(2a)`

we substitute the values

`x=-(0)/(2(-1))=0`

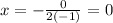
then we substitute the value of x in the equation in order to find the y- coordinate

`\begin{gathered} f(x=0)=0+5 \\ f(x=0)=5 \end{gathered}`

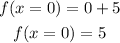
the vertex is (0,5), as we can see the axis of symmetry of the function is the y-axis

the domain is the set of all possible values that can have x, in this case, the domain is

`(-\infty,\infty)`

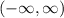
in other words all the real numbers

the range is the set of all possible values that can have f(x)

assuming f(x)=y, we need to isolate x in order to know the range

`x=\sqrt[]{-y+5}`

we can't have negative values in the square root so the range is

`(-\infty,5\rbrack`