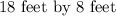Question

The width of a rectangular garden is 2 feet more than one third of its length. The perimeter is 52 feet. Find the dimensions of the rectangle

Answer 1

The dimension of the rectangle is;

`18\text{ feet by 8 feet}`

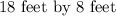
Step-by-step explanation:

Let l and w represent the length and width of the rectangular garden;

Given;

The width of a rectangular garden is 2 feet more than one third of its length;

`w=(l)/(3)+2\text{ -----------1}`

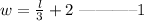
And the perimeter is 52 feet;

The perimeter of a rectangle is;

`\begin{gathered} P=2l+2w=52 \\ 2l+2w=52\text{ ----------2} \end{gathered}`

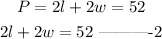
To get l let us substitute equation 1 to 2;

`\begin{gathered} 2l+2w=52 \\ 2l+2((l)/(3)+2)=52 \\ 2l+(2)/(3)l+4=52 \\ 2(2)/(3)l=52-4 \\ l=(48)/(2(2)/(3)) \\ l=18\text{ feet} \end{gathered}`

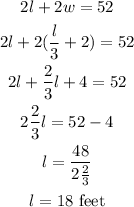
Using equation 1 we can get the value of w;

`\begin{gathered} w=(l)/(3)+2 \\ w=(18)/(3)+2 \\ w=6+2 \\ w=8\text{ feet} \end{gathered}`

Therefore, the dimension of the rectangle is;

`18\text{ feet by 8 feet}`