Question

A committee must be formed with 3 teachers and 7 students. If there are 7 teachers to choose from, and 9 students, how many different ways could the committee be made?

Answer 1

Step 1

The question is combinations because it involved selection.

`^nC_r\text{ = }\frac{n!}{(n\text{ - r)!r!}}`

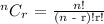
Step 2

Number of ways of selecting 3 teachers out of 7

`\begin{gathered} n\text{ = 7, r = 3} \\ ^7C_3\text{ = }\frac{7!}{(7\text{ - 3)!3!}} \\ =\text{ }(7*6*5*4!)/(4!*3*2*1) \\ =\text{ 35 } \end{gathered}`

Step 3

Number of ways of selecting 7 students out of 9

`\begin{gathered} n=\text{ 9 , r = 7} \\ ^9C_7\text{ = }\frac{9!}{(9\text{ - 7)!7!}} \\ =(9!)/(2!7!) \\ =\text{ }(9*8*7!)/(2*1*7!) \\ \text{= 9 }*4 \\ =\text{ 36} \end{gathered}`

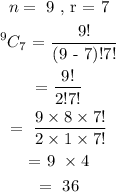
Final answer

Different ways could the committee be made

= 35 x 36

= 1260 ways