Answer:
Step-by-step explanation:
Let's sketch the line segment as seen below;
From the above, we can see that points XYZ are the points that divide the line segment to four equal parts. Let's go ahead and determine their coordinates.
Since point Y is the midpoint of AB, we'll use the midpoint formula to determine its coordinate;
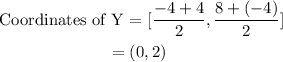
We can see that point X is the midpoint of AY, let's use the midpoint formula too to determine its coordinates;
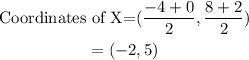
We can see that point Z is the midpoint of YB, let's use the midpoint formula too to determine its coordinates;
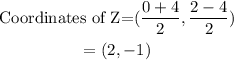
Therefore the coordinates of the