Show x+a is factor of
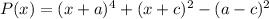
We are going to simplify the expressions (x+c)^2 and (a-c)^2:
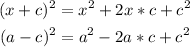
Sustituing:
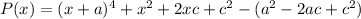

Now we can evaluate if x+a is a factor, x+a is a factor if the polynomial in x+a=0 is a root of p(x), we can see
x=-a
Sustituing:


Simplifying:
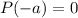
Therefore x+a is a factor of the polynomial P(x).