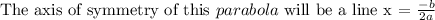Question

Use the quadratic function to determine the sign of the leading coefficient, vertex, and the equation of the axis of symmetry

Answer 1

Step 1:

Write the quadratic function

`ax^2\text{ + bx + c = 0}`

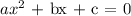
Step 2:

The graph of a quadratic function is a curve called a parabola. Parabolas may open upward or downward and vary in "width" or "steepness", but they all have the same basic "U" shape.

Step 3:

`\text{For ax}^2\text{ + bx + c = 0}`

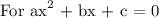
The leading coefficient 'a' is positive, so it opens upwards.

`For-ax^2\text{ + bx + c = 0}`

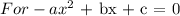
The leading coefficient is '-a' positive, so it opens downwards.

Step 4:

Vertex

`\begin{gathered} \text{The x coordinate of the vertex is x = }(-b)/(2a) \\ Next,\text{ substitute the x into the equation to find the y coordinate.} \end{gathered}`

Step 5:

Equation of the axis of symmetry

Parabolas also have an axis of symmetry, which is parallel to the y-axis. The axis of symmetry is a vertical line drawn through the vertex.

`\text{The axis of symmetry of this }parabola\text{ will be a line x = }(-b)/(2a)`