Question

Identify the equations that are parallel. select all that apply.

Answer 1

We know that two lines are parallel if they have the same slope.

Then, we can write the given equations of the lines in their slope-intercept form.

`\begin{gathered} y=mx+b \\ \text{ Where} \\ \text{ m is the slope} \\ b\text{ is the y-intercept} \end{gathered}`

Then, we solve for y each equation:

• First equation

`\begin{gathered} 6y-x=14 \\ \text{ Add x from both sides} \\ 6y-x+x=14+x \\ 6y=14+x \\ \text{ Divide by 14 from both sides} \\ (6y)/(6)=(14+x)/(6) \\ y=(14)/(6)+(1)/(6)x \\ \text{ Simplify} \\ y=(7\cdot2)/(3\cdot2)+(1)/(6)x \\ y=(7)/(6)+(1)/(6)x \\ \text{ Reorder} \\ y=(1)/(6)x+(7)/(6) \end{gathered}`

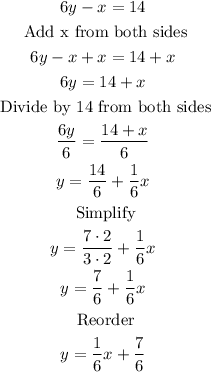
• Second equation

`\begin{gathered} -4y+2x=1 \\ \text{ Subtract 2x from both sides} \\ -4y+2x-2x=1-2x \\ -4y=1-2x \\ \text{ Divide by -4 from both sides} \\ (-4y)/(-4)=(1-2x)/(-4) \\ y=-(1)/(4)+(2x)/(4) \\ y=-(1)/(4)+(1)/(2)x \\ \text{ Reorder} \\ y=(1)/(2)x-(1)/(4) \end{gathered}`

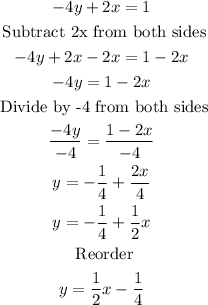
• Third equation

`\begin{gathered} 2y-(1)/(3)x=12 \\ \text{ Add }(1)/(3)x\text{ from both sides} \\ 2y-(1)/(3)x+(1)/(3)x=12+(1)/(3)x \\ 2y=12+(1)/(3)x \\ \text{ Divide by 2 from both sides} \\ (2y)/(2)=(12+(1)/(3)x)/(2) \\ y=(12)/(2)+((1)/(3))/(2)x \\ y=6+((1)/(3))/((2)/(1))x \\ y=6+(1\cdot1)/(3\cdot2)x \\ y=6+(1)/(6)x \\ \text{ Reorder} \\ y=(1)/(6)x+6 \end{gathered}`

• Fourth equation

`\begin{gathered} 5x+3y=1 \\ \text{ Subtract 5x from both sides} \\ 5x+3y-5x=1-5x \\ 3y=1-5x \\ \text{ Divide by 3 from both sides} \\ (3y)/(3)=(1-5x)/(3) \\ y=(1)/(3)-(5)/(3)x \\ \text{ Reorder} \\ y=-(5)/(3)x+(1)/(3) \end{gathered}`

Then, the lines have the following slopes:

• First

`m=(1)/(6)`

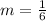
• Second

`m=(1)/(2)`

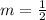
• Third

`m=(1)/(6)`

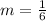
• Fourth

`m=-(5)/(3)`

As we can see, only the first and third lines have the same slope.

Therefore, only the first and third lines are parallel.