We are given the following functions:

We are asked to determine the composite function:

To do that we will replace as the value of "x" in g(x) the function f(x), like this:
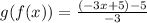
Therefore, the numerator of the composite function is:
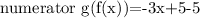
And the denominator is:
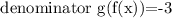
Now we simplify the fraction, first by canceling out the 5:
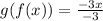
Now we cancel out the -3:
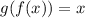
Since the composite function is "x" this means that the functions are inverses of each other.