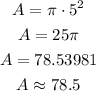Question

Graph the circle with center (-3, -3) that passes through (2, -3). Find the area in terms of r and to the nearesttenth. Use 3.14 for Ñ

Answer 1

The standard equation of a circle is the following:

`r^2=(x-h)^2+(y-k)^2`

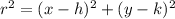
where (h,k) is the center and (x,y) can be any point

In this example, (h,k) = (-3,-3)

and, (x,y) = (2,-3)

using this information we can calculate the radius r

`\begin{gathered} r^2=(2+3)^2+(-3+3)^2 \\ r^2=5^2+0 \\ r^2=5^2 \\ r=5 \end{gathered}`

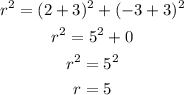
therefore, the standard equation for this circle is:

`5^2=(x+3)^2+(y+3)^2`

and this can be graph as it follows:

now, the area in terms of r for a circle is

`A=\pi r^2`

So, the area for this circle is 78.5

`\begin{gathered} A=\pi\cdot5^2 \\ A=25\pi \\ A=78.53981 \\ A\approx78.5 \end{gathered}`