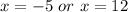The polynomial is given to be:
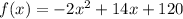
FACTORING THE POLYNOMIAL
Step 1: Multiply the first and last term of the polynomial and get two numbers that will multiply to give the result and will add up to the middle term
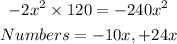
Step 2: Replace the middle term with the two numbers gotten in Step 1 above
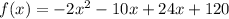
Step 3: Factor out the common term in each pair of numbers as shown below
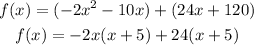
Step 4: Factor out the common term (x + 5)
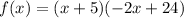
Step 5: Factor out -2x from the term (-2x + 24)
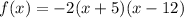
The factored polynomial is:
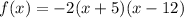
ZEROES OF THE FUNCTION
The zeroes of the function are gotten at f(x) = 0
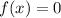
Therefore, we have that:
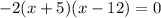
Recall the Zero Factor Principle:
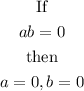
Therefore, we have that:
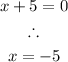
or
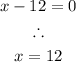
Therefore, the zeroes of the function are: