The formula to calculate the standard deviation is given to be:
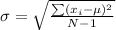
where
σ = population standard deviation
N = the size of the population
xi = each value from the population
μ = the population mean
The mean of the data set is calculated as follows:
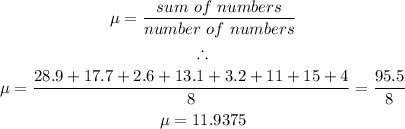
Using a calculator, we have the sum of squares to be:
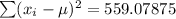
There are 8 data. Therefore, the standard deviation is calculated to be:
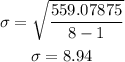
The standard deviation is 8.94.