The inequality can be decomposed into two inequalities.
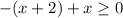
and
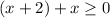
This is because |x+2| = |-(x+2)|.
Let us first solve the first inequality by first simplifying it
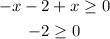
it has no solutions.
Let us now turn to the second inequality which simplifies to

subtracting 2 from both sides and then dividing both sides by 2 gives

which is our answer!