When you are looking for a line perpendicular to a known line, you have to keep in mind that the slope of the permendicular line will be the inverse negative of the first line.
So for the given line:
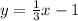
The slope is m=1/3
The slope for the perpendicular will be the inverse negative:
m=-3
Using this slope and the given point (2, 4), you can apply the point-slope formula to determine de equation of the perpendicular line.

Replace it with the point coordinates and the slope:
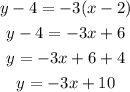
The equation for the perpendicular line is y=-3x+10 and the correct choice is the last one.