A parallelogram:
Opposite angles are equal.
Opposite sides are equal and parallel.
Diagonals bisect each other.
Sum of any two adjacent angles is 180°
A rectangle:
All the angles of a rectangle are 90°
Opposite sides of a rectangle are equal and Parallel.
Diagonals of a rectangle bisect each other.
A rhombus:
Opposite angles are equal.
All sides are equal and, opposite sides are parallel to each other.
Diagonals bisect each other perpendicularly.
Sum of any two adjacent angles is 180°
A square:
The diagonals of a square bisect each other and meet at 90°.
The diagonals of a square bisect its angles.
Opposite sides of a square are both parallel and equal in length.
All four angles of a square are equal
All four sides of a square are equal.
According to the figure:
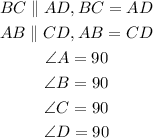
Therefore, we can conclude that the figure is a rectangle and a parallelogram