Question

Find the displacement from (pi/2,2pi) and find the total distance traveled from (pi/2,2pi)

Answer 1

Displacement and Distance

Given the velocity function, we can calculate the displacement by integrating this function without any restriction of the endpoints, because we won't care about signs of the results. The displacement can be positive, negative, or even zero because it measures the change of position and NOT the distance traveled.

That said, integrate the velocity function as follows:

`X=\int ^(2\pi)_{(\pi)/(2)}-5\sin tdt`

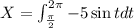
Integrating:

`\begin{gathered} X=5\cos t\begin{cases}2\pi \\ (\pi)/(2)\end{cases} \\ X=5\cos 2\pi-5\cos (\pi)/(2) \\ X=5-0=5 \end{gathered}`

The displacement is 5 ft

Now for the distance, we must be careful with the sign of the function in the given interval. It's convenient to graph the function as follows:

The function changes its sign from negative to positive at x = π. Since the distance is always positive, we must add the positive and the negative area with its absolute values.

Separating the integral:

`D=\int ^(\pi)_{(\pi)/(2)}5\sin tdt-\int ^(2\pi)_(\pi)5\sin tdt`

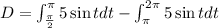
Integrating:

`\begin{gathered} D=-5\cos t\begin{cases}\pi \\ (\pi)/(2)\end{cases}+5\cos t\begin{cases}2\pi \\ \pi\end{cases} \\ D=-5(\cos \pi-\cos (\pi)/(2))+5(\cos 2\pi-\cos \pi) \\ D=-5(-1-0)+5(1+1) \\ D=15\text{ ft} \end{gathered}`

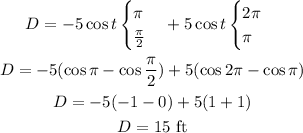
The distance is 15 ft