Question

A lamp has the shape of a parabola when viewed from the side. The light source (which is at the focus) is 5 centimeters from the bottom of the lamp and thelamp is 20 centimeters deep. How wide is the lamp?

Answer 1

we know that

Te equation of a vertical parabola is

`y=A(x-h)^2+k`

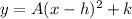
where

A is the leading coefficient

(h,k) is the vertex

In this problem

(h,k)=(0,0)

so

`y=Ax^2`

we have that

For x=a, y=20 -----> is given

substitute

`\begin{gathered} 20=A(a)^2 \\ A=(20)/(a^2) \end{gathered}`

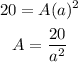
therefore

the equation is

`y=((20)/(a^2))x^2`

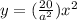
Remember that

the equation of the parabola in standard form is equal to

(x − h) 2 = 4 p (y − k)

vertex is (0,0)

so

x^2=4py

where

p is the distance between the vertex and the focus

in this problem

p=5

substitute

x^2=4(5)y

x^2=20y

y=(1/20)x^2

Compare this equation with the previous equation

so

`(1)/(20)=(20)/(a^2)`

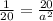
solve for a

`\begin{gathered} a^2=20^2 \\ a=20 \end{gathered}`

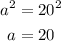
therefore

the wide of the lamp is 2a

so

2(20)=40 cm

the answer is 40 cm