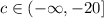Consider the given inequation,
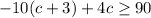
Resolve the parenthesis first,
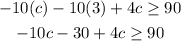
Adding the like terms,
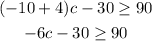
Add 30 both sides,
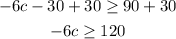
Divide both sides by -6, note that the inequality gets reversed when multiplied or divided by a negative number,
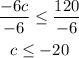
Thus, the solution set for the given inequation is,