Taking x and y as the integers.
Let's say that x is 4 less than twice y. This is:

The sum of the squares of x and y is 544, this is:
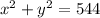
Use the first equation and replace this expression for the value of x in the second equation:

Solve the quadratic equation
![\begin{gathered} y=\frac{16\pm\sqrt[]{16^2-4(5\cdot-528)}}{2\cdot5} \\ y=(16\pm104)/(10) \\ y1=(16+104)/(10)=(120)/(10)=12 \\ y2=(16-104)/(10)=-(44)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x6gtkhva3g4nbdhzyqi4xebx87dccr2b6w.png)
y can take 2 values, but, as we know, x and y must be positive integers, the value of y that meets this condition is 12. It means one of the integer is 12.
Use this value and the first equation to find the second integer:
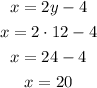
The integers are 20 and 12.