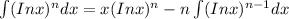Question

Been practicing this type of questions several times and I i just need a little detailed solution because I'm practicing for an upcoming exam

Answer 1

2.1

`\int (Inx)^ndx`

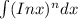
This can be written as :

`\int 1.(Inx)^ndx`

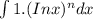
The formula for the integration by part is given by:

`\text{Udv}=uv-\int Vdu`

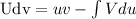
Let U = (Inx)ⁿ and dv = 1

We are going to differentiate U and integrate dv ( with respect to x)

That is;

`\begin{gathered} (du)/(dx)=(Inx)^(n-1).(1)/(x) \\ \\ \Rightarrow du=n(Inx)^(n-1)\text{.}(1)/(x)dx \end{gathered}`
`\begin{gathered} dv=1dx \\ \int 1dx\text{ = x} \end{gathered}`

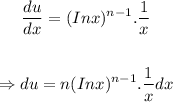
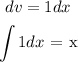
We can now proceed to substitute into the formula;

`\int (Inx)^n.1dx=^{}(Inx)^n.x-\int n(Inx)^(n-1)dx`

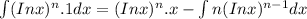
We can bring out n on the right-hand side since it is a constant.

`\int (Inx)^ndx=x(Inx)^n-n\int (Inx)^(n-1)dx`