Given the equations:
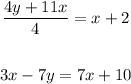
Let's determine if the lines are parallel or perpendicular.
Rewrite both equations in slope-intercept form:
y = mx + b
Where m is the slope.
Rewrite each equation for y.
• Equation 1:

• Equation 2:

Therefore, we have both equations in slope-intercept form:
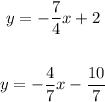
• The slope of equation 1 is: -7/4
,
• The slope of equation 2 is: -4/7
Parallel lines have equal slopes.
Perpendicular lines have slopes that are the negative reciprocal of each other.
Since both slopes are neither equal nor negative reciprocals, then both lines are neither parallel nor perpendicular.
• ANSWER:
Neither