Question

Please choose the coordinate plane below to help find the missing point

Answer 1

Let's graph the 3 points given and name them accordingly.

The 3 points given are:

A = (-4, 3)

B = (4, 3)

C = (2, -3)

and the fourth point (the other vertex), we will label as D(x,y).

Since it is a parallelogram, we can say:

Midpoint AC = Midpoint BD

The midpoint formula between two points (x1, y1) and (x2, y2) is,

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

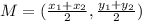
This is basically the average of the x points and the average of the y points.

Now,

• Let's find ,midpoint AC,,

`\begin{gathered} A=(-4,3) \\ C=(2,-3) \\ ---------- \\ \text{Midpoint of AC,} \\ ((-4+2)/(2),(3-3)/(2))=(-1,0) \end{gathered}`

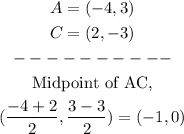
• Let's find the expression for ,midpoint of BD,,

`\begin{gathered} B=(4,3) \\ D=(x,y) \\ --------- \\ \text{Midpoint of BD,} \\ ((4+x)/(2),(3+y)/(2)) \end{gathered}`

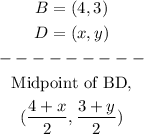
Since MIDPOINT AC = MIDPOINT BD, we can find x and y easily:

`\begin{gathered} (4+x)/(2)=-1 \\ 4+x=-2 \\ x=-2-4 \\ x=-6 \\ ----------- \\ (3+y)/(2)=0 \\ 3+y=0 \\ y=-3 \end{gathered}`

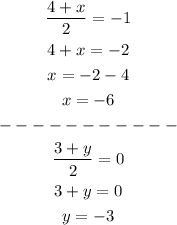
Thus, the fourth coordinate is (x, y) = (-6, -3)

Answer(-6, -3)