Question

A sealed syringe is filled with 30 cm^3 of air at a temperature of 29 °C. Thesyringe is cooled to 4 °C in a freezer. What is the new volume of the air?Assume the air pressure inside is constant.

Answer 1

Given,

The initial volume of the air, V₁=30 cm³=30×10⁻6 m³

The initial temperature of the air, T₁=29 °C=302.15 K

The final temperature of the air, T₂=4 °C=277.15 K

From Charles' law, we have,

`(V_1)/(T_1)=(V_2)/(T_2)`

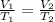
Where V₂ is the final volume of the air.

On substituting the known values,

`\begin{gathered} (30*10^(-6))/(302.15)=\frac{V_2_{}}{277.15} \\ \Rightarrow V_2=(30*10^(-6)*277.15)/(302.15) \\ =27.52*10^(-6)m^3 \\ =27.52cm^3 \end{gathered}`

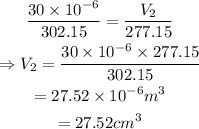
Thus the volume of the ai after reducing the temperature is 27.52 cm³