Question

A line segment has the endpoint T(2,4) and the Midpoint of (11,6.5) Find the coordinates of the other point B. Write it as a point.

Answer 1

(20, 9)

Step-by-step explanation:

The coordinates of one of the endpoints of the line is: T(2,4)

The midpoint of line segment TB = (11,6.5)

Let the coordinates of B be (x,y).

`\text{Midpoint(11,6.5)}=\mleft((2+x)/(2),(4+y)/(2)\mright)`

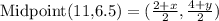
We then solve for x and y.

`\begin{gathered} 11=(2+x)/(2) \\ x+2=22 \\ x=22-2 \\ x=20 \end{gathered}`

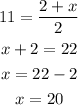
Similarly

`\begin{gathered} 6.5=(4+y)/(2) \\ y+4=13 \\ y=13-4 \\ y=9 \end{gathered}`

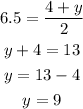
The coordinates of the other point B is (20, 9)