Question

Write the rule for the function g(x)g(x) reflects f(x)=2(x-1)^3 +1 across the y-axis and translates 3 units right and 1 unit up

Answer 1

Step-by-step explanation:

The original function is f(x):

`f(x)=2(x-1)^3+1`

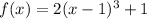
And g(x) is the transformed function after a reflection across the y-axis, a translation of 3 units right and 1 unit up.

Step 1. A reflection across the y-axis is represented by:

`f(x)\rightarrow f(-x)`

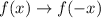
Step 2. A translation of 3 units to the right is represented by:

`f(x)\rightarrow f(x+3)`

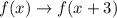
Step 3. And a translation of 1 unit up is represented by:

`f(x)\rightarrow f(x)+1`

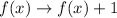
Step 4. Combining these three transformations:

`f(x)\rightarrow f(-x+3)+1`

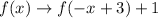
Step 5. Function g(x) is defined as follows:

`g(x)=f(-x+3)+1`

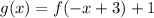
Which applied to the f(x) function is:

`\begin{gathered} f(x)=2(x-1)^(3)+1 \\ \downarrow \\ g(x)=f(-x+3)+1 \\ \downarrow \\ Applying\text{ the transformation:} \\ g(x)=2(-x+3-1)^3+1+1 \end{gathered}`

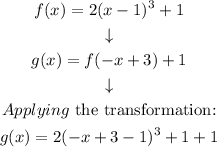
Simplifying the operations:

`g(x)=2(-x+2)^3+2`

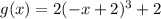
That is the rule for function g(x).

Answer:

`g(x)=2(-x+2)^(3)+2`