Answer:
• (a)Bottom-Heavy, y=0
,
• (b)Equal, y=1/3
,
• (c)Top heavy, No horizontal asymptote
Explanation:
• A Rational function is bottom-heavy when ,the degree of the numerator is less than the degree of the denominator,.
,
• A Rational function is top-heavy when ,the degree of the numerator is more than the degree of the denominator,.
,
• It is balanced (or equal) when ,the degree of the numerator is equal to the degree of the denominator,.
Part A
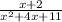
The function is bottom-heavy.
Since the function is bottom-heavy, the horizontal asymptote is:

Part B
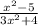
The function is equal.
Since the function is equal, divide the leading coefficients to find the horizontal asymptote.
The horizontal asymptote is at y=1/3.
Part C
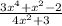
The function is top-heavy.
Since it is top-heavy, it has no horizontal asymptote.