Question

A box with an open top has a square base and four sides of equal height. The volume of the box is 640 ft^3. The height is 2 ft greater than both the length and the width. If the surface area is 384 ft^2, what are the dimensions of the box?

Answer 1

If the base is a square, the length is equal the width (let's call it x).

If the height is 2 ft greater than the length and width, we have:

`h=x+2`

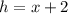
Also, if the surface area is 384 ft², we have:

`\begin{gathered} S=x^2+4\cdot xh \\ 384=x^2+4xh \end{gathered}`

Using h = x + 2 in this equation, we have:

`\begin{gathered} 384=x^2+4x(x+2) \\ 384=x^2+4x^2+8x \\ 384=5x^2+8x \\ 5x^2+8x-384=0 \end{gathered}`

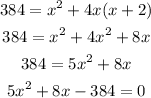
Solving this equation using the quadratic formula, we have:

`\begin{gathered} x_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}=\frac{-8+\sqrt[]{64+7680}}{10}=(-8+88)/(10)=8 \\ x_2=(-8-88)/(10)=-9.6 \end{gathered}`

So if x = 8, the dimensions of the box are 8 ft of length, 8 ft of width and 10 ft of height.