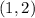The equation of a parabola with vertex (h,k) is given by:
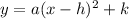
Starting from the given equation, complete the square to write the function in vertex form:
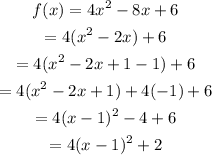
By comparing that equation with the vertex form of a parabola, we can see that h=1 and k=2.
Therefore, the vertex of the given quadratic polynomial, is: