Question

What would I set the scales to also what would be the vertex,roots , and two other points

Answer 1

We have

`y=-x^2-22x-112`

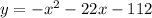
For the vertex we have the next formula

for the x-coordinate of the vertex

`x=(-b)/(2a)`

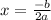
In our case

a=-1

b=-22

`x=(22)/(2(-1))=-11`

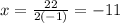
then we substitute this value in the function

`y=-(-11)^2-22(-11)-112=9`

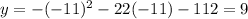
The vertex is (-11,9)

For the roots we make y=0

`\begin{gathered} -x^2-22x-112=0 \\ x^2+22+112=0 \end{gathered}`

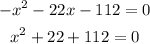
Then we factorize

`(x+14)(x+8)=0`

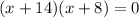
The roots are

x=-14

x=-8

Then for other two points

x=-15

`-(-15)^2-22(-15)-112=-7`

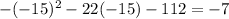
Point (-15,7)

x=-7

`-(-7)^2-22(-7)-112=-7`

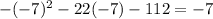
Point (-7,-7)

the x-sel1

the ysel : 2