We have
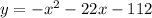
For the vertex we have the next formula
for the x-coordinate of the vertex
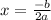
In our case
a=-1
b=-22
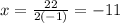
then we substitute this value in the function
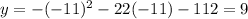
The vertex is (-11,9)
For the roots we make y=0
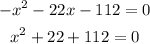
Then we factorize
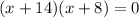
The roots are
x=-14
x=-8
Then for other two points
x=-15
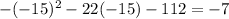
Point (-15,7)
x=-7
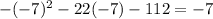
Point (-7,-7)
the x-sel1
the ysel : 2