the estimated fox population in the year 2008 is approximately 24,509 (rounded to the nearest integer).
To find a function that models the population \( t \) years after 2000 with an initial population of 14,000 and a continuous growth rate of 7% per year, we use the formula for continuous growth:
![\[ P(t) = P_0 \cdot e^(rt) \]](https://img.qammunity.org/2023/formulas/mathematics/college/6z78vhqcduzz908s56fumto7xep3kgymeq.png)
where:
-
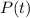 is the population at time
is the population at time
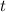 ,
,
-
 is the initial population,
is the initial population,
-
 is the growth rate,
is the growth rate,
-
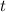 is the time in years since the start (year 2000 in this case),
is the time in years since the start (year 2000 in this case),
-
 is the base of the natural logarithm.
is the base of the natural logarithm.
Given:
-
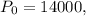
-
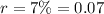 (as a decimal),
(as a decimal),
-
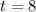 (for the year 2008, since \( 2008 - 2000 = 8 \)).
(for the year 2008, since \( 2008 - 2000 = 8 \)).
The function modeling the population is:
![\[ P(t) = 14000 \cdot e^(0.07t) \]](https://img.qammunity.org/2023/formulas/mathematics/college/wehzp6zvssa6pm7brdpo66g2xjdpeod34h.png)
To estimate the population in the year 2008, we substitute
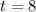 into the function:
into the function:
![\[ P(8) = 14000 \cdot e^(0.07 \cdot 8) \]](https://img.qammunity.org/2023/formulas/mathematics/college/62wctk6qe2e8f89py9zb5wda3e8y4awihl.png)
Calculating this gives us
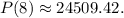
So, the estimated fox population in the year 2008 is approximately 24,509 (rounded to the nearest integer).