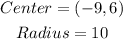Step-by-step explanation:
Given;
We are given the equation of a circle as shown below;
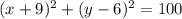
Required;
We are required to use the information provided to calculate the radius and center of the circle.
Step-by-step solution;
The standard equation of a circle is given as follows;
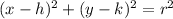
Here, the variables are;
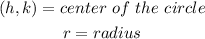
Note that the equation provided here is already in standard form.
Therefore, we can observe the following;
![\begin{gathered} (x+9)^2+(y-6)^2=100 \\ For: \\ (x-h)^2+(y-k)^2=r^2 \\ We\text{ }have: \\ (x-[+9])^2+(y-[-6])^2=√(100) \\ \\ h=-9,k=+6,r=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9olhv0bch46lowu6hj5y4564u7z99imm3a.png)
Therefore;
ANSWER: