Given:
The resistances connected in parallel combination are:
R1 = 14 Ω
R2 = 22 Ω
R3 = 34 Ω
The voltage applied is: V = 52 v dc
To find:
a) The current
b) The power
Step-by-step explanation:
a)
The equivalent resistance R of all three resistors connected in parallel is given as:

Substituting the values in the above equation, we get:
![\begin{gathered} (1)/(R)=\frac{1}{14\text{ \Omega}}+\frac{1}{22\text{ \Omega}}+\frac{1}{34\text{ \Omega}} \\ \\ (1)/(R)=\frac{22}{22*14\text{ \Omega}}+\frac{14}{14*22\text{ \Omega}}+\frac{1}{34\text{ \Omega}} \\ \\ (1)/(R)=\frac{36}{308\text{ \Omega}}+\frac{1}{34\text{ \Omega}} \\ \\ (1)/(R)=\frac{36*34}{34*308\text{ \Omega}}+\frac{308}{308*34\text{ \Omega}} \\ \\ (1)/(R)=\frac{1224}{10472\text{ \Omega}}+\frac{308}{10472\text{ \Omega}} \\ \\ (1)/(R)=\frac{1532}{10472\text{ \Omega}} \\ \\ R=\frac{10472\text{ \Omega}}{1532} \\ \\ R=6.8355\text{ \Omega} \end{gathered}]()
Now, this equivalent resistance R of the parallel combination of resistors acts as a single resistance through which the current I passes when 52 v voltage is applied across it. The current can be calculated by using Ohm's law as:
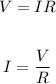
Substituting the values in the above equation, we get:

b)
The power P is given as:
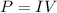
Substituting the values in the above equation, we get:
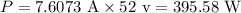
Final answer:
a) The current is 6.8355 Amperes.
b) The power is 395.58 watts.