The diagram provided is a regular hexagon. This means that all the sides and angles are equal.
We can divide the hexagon into 6 parts by drawing diagonals as follows:
For a regular hexagon, all the labelled angles are equal, such that
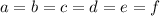
The sum of all the angles is equal to 360°. Therefore, each angle will be equal to

This means that angle ZCX is equal to 60°.
Hence, we can bring out Triangle XCZ from the question:
The base angles are equal since the vertical sides are equal.
Therefore,
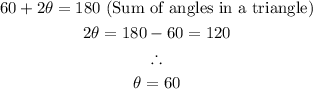
From this, we can get the smaller triangle ZCY and find the angle ZCY as follows:
Therefore, angle ZCY can be calculated as
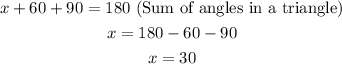
Therefore, the value of angle ZCY is 30°.