Question

An object is assembled using a plastic stick with a length of d has a cube with a mass of m placed at the ends of the stick. The stick-cube assembly is placed on a light swivel. Another cube with a mass of 2m is tied toa thin cord and connected to the swivel. Starting with an initial velocity of zero, the hanging cube is allowed to move downward causing the assembly to rotate. The assembly has a rotational inertia of 1/2 md^2. Consider the stick-cube assembly and hanging mass to be a system. Express all answers in terms of quantities givenand fundamental constants.(a) The hanging cube moves a distance y to the floor. Determine whether the rotational kinetic energy of the stick-cube assembly is greater than, equal to, or less than the quantity 2mgy.Greater than 2mgyEqual to 2mgyLess than 2mgyJustify your answer.(b) Determine the angular speed of the stick-cube assembly.(c) Determine the impulse applied to the stick-cube assembly.(d) Suppose the swivel has significant mass. Determine whether the predicted answer in part (a) would be different. Explain your response.

Answer 1

In the given assembly we have a stick with two masses "m" attached to its end. We are asked the following:

Part A. If the cube of "2m" moves a distance "y" to the floor then, by the principle of conservation of energy this means that the initial gravitational potential energy is converted into the final kinetic energy of the falling mass and the rotational kinetic energy of the assembly. This can be written as follows:

`U_0=K_l+K_r`

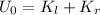
Where:

`\begin{gathered} U_0=\text{ initial gravitational potential energy} \\ K_l=\text{ linear kinetic energy of the falling object} \\ K_r=\text{ rotational kinetic energy of the rotating assembly} \end{gathered}`

The gravitational potential energy is given by:

`U_0=mgy`

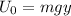
Where:

`\begin{gathered} m=\text{ mass} \\ g=\text{ gravitational constant} \\ y=\text{ height} \end{gathered}`

The mass of the falling object is "2m" therefore:

`U_0=2mgy`

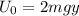
Substituting in the balance of energy:

`2mgy=K_l+K_r`

Now, we can solve for the kinetic energy of the rotating object:

`2mgy-K_l=K_r`

Therefore, the kinetic energy of the assembly is less than "2mgy".

Part B. We are asked to determine the angular speed o the assembly. To do that we will use the following formula for the rotational kinetic energy of the assembly:

`K_r=(1)/(2)I\omega^2`

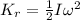
Where:

`\begin{gathered} I=\text{ moment of inertia} \\ \omega=\text{ angular velocity} \end{gathered}`

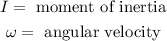
The linear kinetic energy is given by:

`K_l=(1)/(2)mv^2`

Where:

`v=\text{ velocity of the falling mass}`

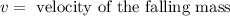
Substituting the mass of the falling object:

`K_l=(1)/(2)(2m)v^2=mv^2`

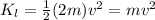
Substituting in the balance of energy:

`2mgy-mv^2=(1)/(2)I\omega^2`

The rotational inertia is given by the following formula:

`I=(1)/(2)md{}^2`

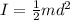
Substituting we get:

`2mgy-mv^2=(1)/(2)((1)/(2)md^2)\omega^2`

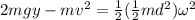
We can cancel out the mass "m":

`2gy-v^2=(1)/(4)d^2\omega^2`

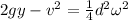
We have that the linear velocity "v" of the falling object is related to the angular velocity of the assembly by the following equation:

`v=\omega r`

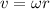
Substituting we get:

`gy-\omega^2r^2=(1)/(4)d^2\omega^2`

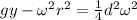
Now, we add the square of the angular velocity and the radius to both sides:

`gy=(1)/(4)d^2\omega^2+\omega^2r^2`

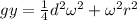
Now, we take the square of the angular velocity as a common factor:

`gy=((1)/(4)d^2+r^2)\omega^2`

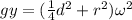
Now, we divide both sides by the factor of the square of the angular velocity:

`(gy)/((1)/(4)d^2+r^2)=\omega^2`

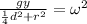
Taking the square root to both sides we get:

`\sqrt{(gy)/((1)/(4)d^2+r^2)}=\omega`

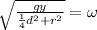
And thus we got the expression to determine the angular velocity.

Part C. The impulse is given by:

`\Delta L=I(\omega_f-\omega_0)`

Where:

`\begin{gathered} \Delta L=\text{ angular impulse} \\ \omega_f,\omega_0=\text{ final and initial angular velocity} \end{gathered}`

If the system starts from rest then the initial angular velocity is zero and the formula reduces to:

`\Delta L=I\omega`

Substituting the expressions:

`\Delta L=(1)/(2)md^2\sqrt{(gy)/((1)/(4)d^2+r^2)}`

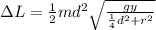
And thus we get an expression to calculate the impulse.

Part D. If the mass of the swivel is "M", then the new balance of energy is:

`2mgy=mv^2+(1)/(2)I\omega^2+(1)/(2)I_s\omega_s^2`

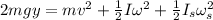
Therefore, the rotational kinetic energy of the assembly would still be less than "2mgy" since the initial gravitational potential energy is converted into the kinetic energy of the falling object and the kinetic energy of the swivel.