Question

Jordan borrowed $10,000 from his friend and paid him back $11,500 in 3years. What compound annual interest rate was Jordan charged by hisfriend?PROVIDE THE DECIMAL (4 DECIMAL PLACES)OR THE PERCENT (2 DECIMAL PLACES) please hurry!!!!

Answer 1

To solve this problem, we're going to use the compound interest formula. The formula for compound interest is

`A=P(1+(r)/(n))^(nt)`

where A is the balance with the interest added, P is the principal balance, r is the interest rate, n is the number of times interest is compounded per time period and t is the number of time periods.

In our problem, we start with $10,000, which represents the principal balance P. After 3 years(our amount of time periods t) Hordan's friend paid him back $11,500, which is the balance with the interest added(A). Since the amount of time is 3 years and the interest was compounded annually, the number of times interest is compounded per time period(n) is equal to 1.

Plugging those values in the formula, we have

`11500=10000(1+(r)/(1))^(1\cdot3)`

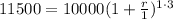
Solving for r, we have

`\begin{gathered} 11500=10000(1+(r)/(1))^(1\cdot3) \\ 11500=10000(1+r)^3 \\ (11500)/(10000)=(1+r)^3 \\ 1.15=(1+r)^3 \\ \sqrt[3]{1.15}=1+r \\ 1.04768955317\ldots=1+r \\ r=1.04768955317\ldots-1 \\ r=0.04768955317\ldots \\ r\approx0.0477=4.77\% \end{gathered}`

And this was the interest rate.