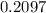Question

A eight sided die which may or may not be a fair dye has four colors on it you have been tossing the die for an hour and have recorded the color rolled for each toss what is the probability you will roll a brown on your next toss of the die express your answer as a simplified fraction or a decimal rounded to four decimal places

Answer 1

Step-by-step explanation:

Step 1:

We will calculate the total number of tosses made within the hour

`\begin{gathered} N=26+49+20+29 \\ N=124 \end{gathered}`

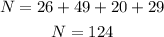
The number of times brown was tossed is given below as

`q=26`

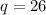
Concept:

At least one of the sides is brown

As you do not know if the die is fair or not, the only way to approximate a probability of rolling a yellow is by making a table of frequencies and record the times you have rolled yellow.

If the number of tosses made in an hour is big enough as to draw a conclusion, then according to the Law of Large Numbers, the probability of rolling a brown in one toss of the die should be

`(q)/(N)`

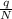
By substituting the values, we will have

`\begin{gathered} (26)/(124)= \\ =0.2097 \end{gathered}`

Hence,

The final answer is

`0.2097`