Question

Write an equation in slope-intercept form of a line passing through the given point andparallel to the given line.13. (4, 2); x+ y= 114. (0,-4);2x+y=315. (5, -3); 4x + 5y = 10

Answer 1

As given by the question

(14)

There are given that the point and the line are:

`(0,\text{ -4) and 2x+y=3}`

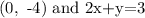
Now,

First, rewrite the given equation of a line in the form of slope-intercept to find the slope.

Then,

From the given equation of line:

`\begin{gathered} 2x+y=3 \\ 2x+y-2x=3-2x \\ y=3-2x \\ y=-2x+3 \end{gathered}`

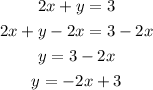
So, the slope is - 2.

Now,

According to the concept of a straight line:

The slope of the parallel lines are same as the slope of the first line

Then,

The slope of the parallel lines is also -2.

Now,

By using the above slope and given point, finding the equation of a line

Then,

From the slope-intercept form:

`y=mx+b`

Then,

Put x = 0, y = -4, and m = -2 into the above equation formula to find the value of b.

So,

`\begin{gathered} y=mx+b \\ -4=-2(0)+b \\ b=-4 \end{gathered}`

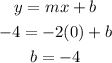
Then,

Put the value of b and m into the slope-intercept form:

So,

`\begin{gathered} y=mx+b \\ y=-2x+(-4) \\ y=-2x-4 \end{gathered}`

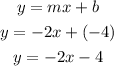
Hence, the equation of line is y = -2x - 4.