Question

A closed organ pipe has a fundamental frequency of 660 Hz, when filled with air. What would its fundamental frequency be if it were filled with helium (speed of sound in helium at 20oC = 927 m/s)?

Answer 1

Answer:

The fundamental frequency will increase to 1782.69 Hz

Step-by-step explanation:

Fundamental frequency of the pipe when filled with air:

`f_{\text{air}}=660Hz`

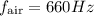
Speed of sound in air:

`v_{\text{air}}=343\text{ m/s}`

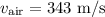
The wavelength is calculated as shown below

`\begin{gathered} v_{\text{air}}=\lambda f_(air) \\ 343=\lambda(660) \\ \lambda=(343)/(660) \\ \lambda=0.52m \end{gathered}`

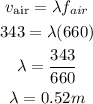
If the closed pipe is filled with helium

Speed of sound in Helium

`v_(He)=927\text{ m/s}`

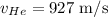
The new fundamental frequency is calculated below:

`\begin{gathered} v_(He)=\lambda f_(He) \\ 927=0.52f_(He) \\ f_(He)=(927)/(0.52) \\ f_(He)=1782.69Hz \end{gathered}`

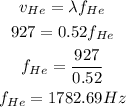
As seen from the calculation above, the fundamental frequency will increase if the closed piper is filled with helium