Answer
The intervals of the averages of the two players do not overlap, it can be concluded that the difference between the two means is statistically significant.
Step-by-step explanation
For Lebron James:
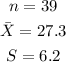
Confidence Interval, CI formula is given by:
![\begin{gathered} CI=\bar{X}\pm z\frac{S}{\sqrt[]{n}} \\ \text{Put the values of }\bar{X},S,n,and\text{ z }=1.960\text{ into the formula} \\ CI=27.3\pm1.960*\frac{6.2}{\sqrt[]{39}} \\ CI=27.3\pm1.960*(6.2)/(6.245) \\ CI=27.3\pm(12.152)/(6.245) \\ CI=27.3\pm1.946_{} \\ CI=(27.3-1.946,27.3+1.946_{}) \\ CI=(25.354,29.264) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2g5skr0mdpt4dbwj9i1e0nmnsp56bvu0mj.png)
For Kwai Leonard:
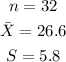
Using the Confidence Interval, CI formula:
![\begin{gathered} CI=\bar{X}\pm z\frac{S}{\sqrt[]{n}} \\ \text{Put the values of }\bar{X},S,n,and\text{ z }=1.960\text{ into the formula} \\ CI=26.6\pm1.960*\frac{5.8}{\sqrt[]{32}} \\ CI=26.6\pm1.960*(5.8)/(5.657) \\ CI=26.6\pm(11.368)/(5.657) \\ CI=26.6\pm2.010 \\ CI=(26.6-2.010,26.6+2.010) \\ CI=(24.59,28.61) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/toslemyod6tj5qmj51uhdhgm9rgejjffcq.png)
To compare the two players, when it comes to points per game;
Lebron James's possible least points per game is 25.354 and the highest possible points per game is 29.264.
Kwai Leonard's possible least points per game is 24.59 and the highest points per game is 28.61.
Thus, since these intervals do not overlap, it can be concluded that the difference between the two means is statistically significant.