Question

Consider the non-right triangle below.Suppose that m∠ACB=97∘ and m∠BAC=47∘, and that y=51.2 cm. What is the value of x?x=

Answer 1

The length of the side x is 63.652.

Given:

Angle C = 97 degree.

Angle A = 47 degree.

The length of the side y is, 51.2 cm.

The objective is to find the length of the side x.

Consider the third side of the triangle as z.

By law of sines,

`(x)/(\sin A)=(y)/(\sin B)=(z)/(\sin C)`

The measure of angle B can be calculated by angle sum property of triangle.

`\begin{gathered} \angle A+\angle B+\angle C=180^0 \\ 47^0+\angle B+97^0=180^0 \\ \angle B=180^0-47^0-97^0 \\ \angle B=36^0 \end{gathered}`

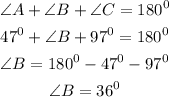
Now the value of x can be calculated by substituting the obtained values in the first two ratios of law of sines.

`\begin{gathered} (x)/(\sin47^0)=(51.2)/(\sin36^0) \\ (x)/(0.731)=(51.2)/(0.588) \\ x=(51.2)/(0.588)\cdot0.731 \\ x=63.652 \end{gathered}`

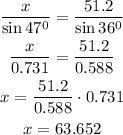
Hence, the length of the side x is 63.652.