Question

Sandra is paid $17.25 an hour to write basic computer programs. She also earns $75 for everyprogram that she finishes.Make and solve an equation to find the amount of programs made (2) given that she earned $813over one 8-hour shift.

Answer 1

We define the following variables:

• m = m(x,y) = money earned,

,

• x = number of hours worked,

,

• y = number of programs made.

From the statement, we know that Sandra earns:

• $17.25 per hour by writing computer programs,

• $75 for every program that she finishes.

Using this data, we write the following equation for the money earned:

`m(x,y)=\text{ \$17.25 }\cdot x+\text{ \$75 }\cdot y.`

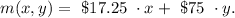
We know that she earned m = $813, and she worked x = 8 hours. We want to know how many programs she made (y). To do that, we replace these data in the equation above, so we have:

`\text{ \$}813=\text{ \$17.25}\cdot8+\text{ \$75}\cdot y.`

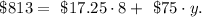
Solving for the variable y, we get:

`\begin{gathered} 813=17.25\cdot8+75\cdot y, \\ 813=138+75\cdot y, \\ 75\cdot y=813-138, \\ 75\cdot y=675, \\ y=(675)/(75)=9. \end{gathered}`

We have that Sandra made y = 9 programs in her shift.

Answer

Sandra made 9 programs in her shift.