Answer
Mass of (H30)2CrO = 38 g
Step-by-step explanation
Given:
Mass of Sn(CrO4)2 = 43.4 g
Mass of (H3O)2HPO4 = 35.2 g
Required: The mass of (H30)2CrO4 that will be produced
Solution:
Calculate the possible mass that could be produced by each reactant, so as to determine the limiting reagent. Use stoichiometry.
For Sn(CrO4)2:
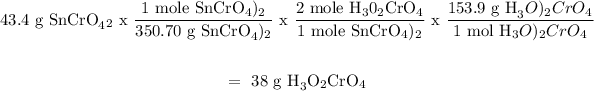
For (H3O)2HPO4
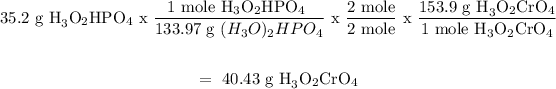
Sn(CrO4)2 will produce less (H30)2CrO4 therefore, Sn(CrO4)2 is the limiting reagent.