Answer:
(a). 423.45 km
(b) 19.88 degrees north of west
Step-by-step explanation:
Let us sketch the displacement of the plane.
Part a.
From the above diagram, we can see that the straight line distance between A and C is the green line.
The angle ABC from geometry we find to be 180° - 36° = 144°.
Therefore, the law of cosines says
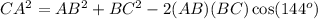
Since AB = 200 and BC = 245, the above gives
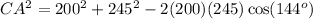
Which upon simplification gives
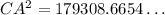
Taking the square root and rounding to two decimal places gives
![\boxed{CA=423.45\operatorname{km}\text{.}}]()
Hence, the straight line distance from A to C is 423.45 km.
Part b.
Finding the direction means we have to find the angle CAB in the above diagram. To do this, we again use the law of cosines.
Let us first rename CAB so that it is easy to write.
Let us call ∠CAB = x
Then the law of cosines gives
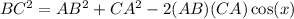
since BC = 245, AB = 200, and CA = 423.45, the above gives
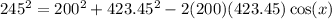
then we solve for cos (x):
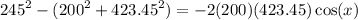
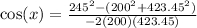
which we evaluate to get
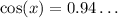
taking the inverse cosine gives
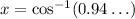
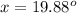
Or in other words,

part (c).
The answer to (a) and (b) are approximately correct because in each case we had to round our answer to appropriate decimal places. It is this rounding that makes us lose our accuracy in our answers.