
THE CORRECT OPTIONS ARE: A, E and F
First one is correct
Let's see if it is increasing.
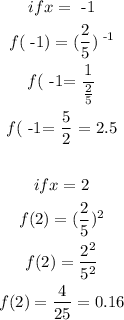
So, it is decreasing. B is incorrect.
3) The x-intercept is 0.
To find the x-intercept we need to make f(x)=0
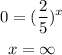
There is no X number which makes the equation 0. It has no X intercept. C is incorrect
D) the domain is x>0. Wrong. I made x = -1 in the example above, and it exists. So it is incorrect.
E) It is decreasing. Correct
F)The range is y>0. Correct. For any number in an exponential function, the range is always going to be a positive number different than 0, because range (0, infinite)