Question

The length of a rectangle is 9 feet more than the width. If the perimeter is 174 feet, what are the length and the width?

Answer 1

`w=39,l=48`

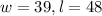
1) Given that, we can write out the following:

l=w+9

Perimeter (2P)= 2(w+l)

2) So now, let's plug into the Perimeter equation the given data:

`\begin{gathered} 2P=2(w+l) \\ 174=2(w+w+9) \\ 2(2w+9)=174 \\ 4w+18=174 \\ 4w+18-18=174-18 \\ 4w=156 \\ (4w)/(4)=(156)/(4) \\ w=39 \end{gathered}`

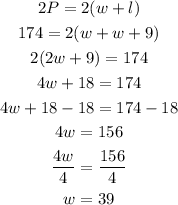
Note that now, we've got the width. So let's plug it back into the first equation to get the length of the rectangle:

`\begin{gathered} l=w+9 \\ l=39+9 \\ l=48 \end{gathered}`

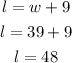
Thus, the width is 39 ft and the length is 48 ft