In the given question, we are asked to explain what the end behavior of the given function tells you about the situation as x gets larger and larger.
Step-by-step explanation
The function is given as;
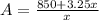
The end behavior is gotten as x tends to infinity
Therefore,
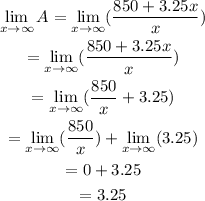
Answer:
Therefore as x gets larger and larger, the function tends towards 3.25