A) 10 units
B) M =(0,4)
A) Since line AB has those endpoints let's apply the distance formula so that we can find out the length AB:
![d_(AB)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/642xnrlbze0ne0ao38qg8ume3bd0uenl70.png)
Now we can plug into that points A and B:
![\begin{gathered} d_(AB)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d_(AB)=\sqrt[]{(-4_{}-4_{})^2+(1_{}-7)^2} \\ d_(AB)=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9jm1hcuscs3lj4k3twerggqxtc99a1npvz.png)
B) To find out the midpoint we must use the following formula:
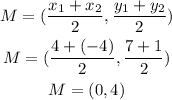
Hence, the answers are
A) 10 units
B) M =(0,4)