Logistic Growth Model
It's commonly used to model population growth in a variety of fields of science.
The formula to calculate the population after a time t is given by:
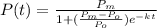
Where Pm is the maximum value of P, k is the growth rate, Po is the initial value of P, and t is the time.
The values taken from the question are Pm=2700, Po = 275, k=35%=0.35, t=2
Substituting and calculating:
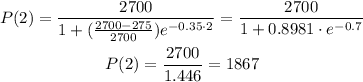
The estimated number of trout after 2 years is 1867