Question

(1 point) Suppose 2' is a normally distributed random variable with u = 10.3 and 0 = 3.8. For the following probability,draw an appropriate diagram, shade the appropriate region and then determine the value:P(9 < 2 ≤ 14) =

Answer 1

Recall the z score formula:

In this case:

`\mu=10.3\text{ and }\sigma=3.8`

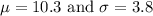
Therefore:

`z=(x-\mu)/(\sigma)`

Calculate the z score for x = 9:

`\begin{gathered} z_1=(9-10.3)/(3.8) \\ z_1=-0.3421 \end{gathered}`

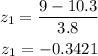
Similarly, the z score of 14 is:

`z_2=(14-10.3)/(3.8)=0.9737`

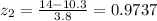
The required diagram is shown.

And the required probability:

P(9 ≤ x ≤ 14) = P(-0.3421 ≤ z ≤ 0.9737) =

Therefore, the correct answer is:

0.4688.