Problem Statement
The question asks us why the quotient of the division of two fractions is greater than the dividing fractions.
Solution
The reasons for this is that:
1. A number in the denominator is the same as multiplying by the reciprocal of that number.
That is,
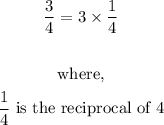
2. Multiplying by the reciprocal of a fraction makes the fraction become greater than 1. That is,
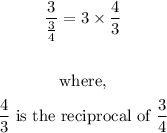
3. This, therefore, has the effect of multiplying a fraction by a number bigger than 1 to give a larger answer because of the multiplication operation rather than the lower value as expected in a division operation.